
Finding eigenvalues and eigenvectors is an important technique in many areas. For example, a classic problem in physics is to find the frequencies of a spring (oscillator) from the eigenvalues of the mathematical description. In cutting edge research on atomic structures, the determination of eigenvalues and eigenvectors often plays a central role (see example at Pacific Northwest Laboratory). As a result, mathematical software to solve this problem has become one of the important computational kernels in linear algebra. One of the early libraries for linear algebra was EISPACK, which solved a variety of types of eigenproblems.
A key class of problems is the solution of the symmetric eigenproblem. This problem arises in many applications since the eigenvalues are always real numbers and physically observable values are real. (This is in contrast to the non-symmetric eigenproblem where the eigenvalues are typically complex numbers.) Since before the advent of EISPACK, the method of choice for solving the symmetric eigenproblem is the QR algorithm. It has the very desirable property that it is provably stable, that is, it always generates the correct answer. Furthermore, Fortran libraries exist which are efficient on everything from workstations to vector supercomputers. The continued importance of this algorithm is shown by its inclusion in the recent LAPACK project which updated libraries for linear algebra.
Recently, a number of the important applications which utilize the symmetric eigenproblem have turned to parallel computers to allow for the solution of larger and more realistic problems. The difficulty encountered is that the QR algorithm has proven difficult to run efficiently on parallel computers. This arises from necessary steps in the algorithm which have proven to be sequential bottlenecks and therefore resisted effective use of parallelism. As a result, the QR algorithm is currently only efficient up to a few processors. This makes it unsuitable for the massively parallel computers of interest in solving many computational problems.
Several research groups are attempting to develop libraries for solving the symmetric eigenproblem which would be efficient on massively parallel computers. Our effort, the PRISM (Parallel Research on Invariant Subspace Methods) project is investigating a new mathematical algorithm based on the work of Auslander and Tsao. Our approach has the same desirable property as the QR algorithm in that it accurately finds the solution in all known cases. Furthermore, unlike the QR algorithm, it is based on computational kernels that allow for efficient implementations on massively parallel computers. As a result, the PRISM symmetric eigensolver has shown to be a viable option as a key library for the solution of large, cutting edge scientific problems.
Since the beginning of the PRISM project, a primary goal has been to supply software to application users. To meet the needs of a diverse set of users necessitates that the PRISM library run on the full range of parallel computers. To achieve this goal, the initial PRISM software utilized the Chameleon communication package by Bill Gropp and Barry Smith from Argonne National Laboratory. This package allows programs to be written in a machine independent manner while still providing very fast performance on all the parallel machines.
A recent development in the parallel computing community is the availability of MPI (Message Passing Interface). This standard is now supported by all the major suppliers of MPPs (Massively Parallel Processors) as well as public domain versions such as the one provided by Argonne National Laboratory and Mississippi State University. As a result, using MPI to achieve portable message-passing code is now the option of choice. In the past year, all the PRISM software has been converted to use MPI. As a result, our eigensolver library now runs on all platforms of interest to the application user. This includes MPPs (IBM SP2, Cray T3D, Intel Paragon, ...) to Network of Workstations (NOWs). The public domain PRISM library comes with verification software to assure the end user that the library is working properly on their particular computer. The User's Guide and the latest version of PRISM software are available in this web site.
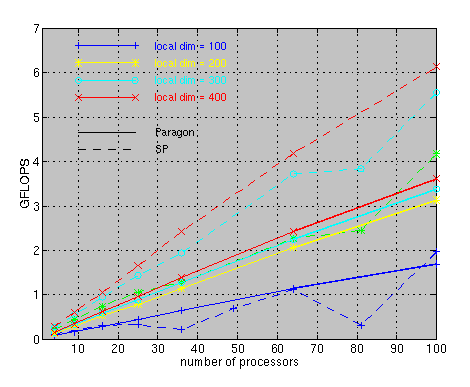
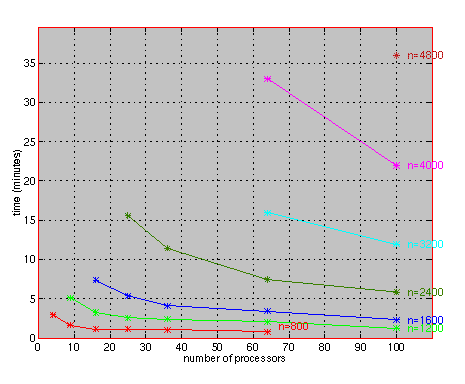
The PRISM symmetric eigensolver has been run on a wide variety of parallel machines. The results in the figure below show the total performance of the PRISM eigensolver in GFLOPS (Billion of Floating Point Operations per Second) on the Argonne SP and Caltech Paragon. The points on the same line represent a constant size problem per node. For example, a local dimension of 400 on 64 processors (8x8 grid) solves a matrix of order 3200 whereas on 100 processors solves a matrix of order 4000. The figure shows that as the local dimension grows, the performance per node is substantially larger for the SP than the Paragon. For example, for local dimension of 400 on 100 processors, the SP achieves over 6 GFLOPS whereas the Paragon achieves only slighter greater than half this performance. This is consistent with the fact that the SP uses RS6000 compute nodes whose peak rating is faster than that of the Paragon's i860 processor. The PRISM eigensolver, which is based on matrix multiplication, is able to effectively utilize these processors to achieve performance which is a substantial fraction of the total peak speed of the machine.